sklearn Identity-transformer

Note: I’ve got a jupyter notebook on my GitHub if you want to just dive into the code.

tl;dr: I self-rolled an sklearn transformer that doesn’t do anything to the input. That allows me to concatenate it to (a transform of) itself using sklearn’s FeatureUnion. This may be practical for debugging/understanding purposes.

Introduction

Since taking Andrew Ng’s course on Machine Learning, I’ve been familiarizing myself with Python’s sklearn. The best way to understand is to get coding, and what better place to start than Kaggle’s Titanic challenge? The biggest value in Kaggle’s dataset is actually the amount of write-ups there’s been on working through the dataset and getting to know it. Two of my favorites are the blogpost by Ahmed Besbes and the Ultraviolet Analytics blogpost series.

The problem

However, these write ups show their age, especially in the way they are constructed. Working through them, I systematically ran into two issues:

• The code was poorly organized. Both workflows seemed to consist of just daisy chaining lines of code. This made for hard readability of the code itself, while making fine tuning of the parameters unnecessarily convoluted by having to execute parts of the code all over again. Additionally, changing the order of the transformations was a task in itself, and not exactly good use of my time.
• Almost no write-up seemed worried about cross-validation, and leaking information from the training set into the CV set. Additionally, the sequential way in which the code was set up didn’t allow for proper grid searching when fine tuning hyper parameters, or even consistent performance analysis of the model.

While racking my brain for how I would implement/solve these issues myself, and going through the sklearn user’s guide (awesome resource by the way, though a little light on explanations sometimes) I came across their Pipeline/FeatureUnion concepts.
These are pretty awesome tools. They allow for a simple, declarative interface, that takes data in, puts it through some clearly defined “transformers”, and ends up putting it through a classifier (usually anyways). It’s got an excellent way to declare parameters, and allows for a simple and clean way to implement cross-validation grid search for hyperparameter tuning for example.

I’m not going to go into detail on what these are and how to use them. There’s some good blog posts out there already that detail it pretty decently. I’ll still be covering the basic stuff, but instead of going into details, I want to show how I used Pipeline/FeatureUnion to self-roll a Transformer that is equivalent to an identity matrix in functionality, and show why that may be useful.

Learn by doing: Titanic cabin transformation

The best way to explain all of this would be through an example (again, check out the notebook on my GitHub if you want to follow along). In the Kaggle Titanic dataset, there is a column named Cabin. It’s a mess of missing and over-filled alphanumeric elements, and our task is to clean it up into something “‘machine learnable”. Most of the write-ups will do two things to it:

• Impute missing values
• Factorize or one-hot-encode it

Intuitively, you can see a pipeline appear here: take the data, put it through the ‘imputer’ transformer, then through the ‘factorizer/one hot encoder’ transformer. However, I wanted to do something unusual for debugging purposes and to better understand how this data-wrangling worked. I wanted to compare the outputs of both transformers side by side. However, sklearn’s FeatureUnions don’t really allow for this. It’s hard to explain though, so hold on.

The way Pipelines work, is that they take an input, transform it in some way, and return the output. Sometimes, you want to do different transformations with different inputs, and concatenate them later, to feed into a classifier. That’s where the FeatureUnion comes in, it simply concatenates (along axis=1) outputs of different Pipelines.

Concatenation shenanigans

But what if I want to concatenate a Pipeline output with a transformed version of itself? I could just concatenate the two pipelines, but then I’m doing the same transformation twice, that’s inefficient.

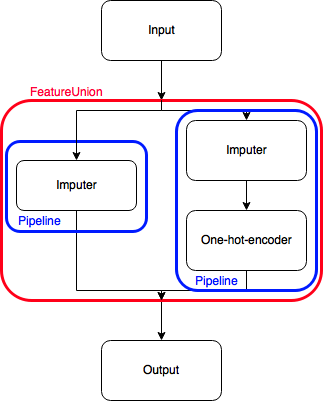
Hence, I figured some kind of identity-Transformer could help out. Its functioning is similar to the identity matrix (hence its name): multiplying a matrix by it doesn’t do anything. That seems relatively pointless, but it allows me to do the following:

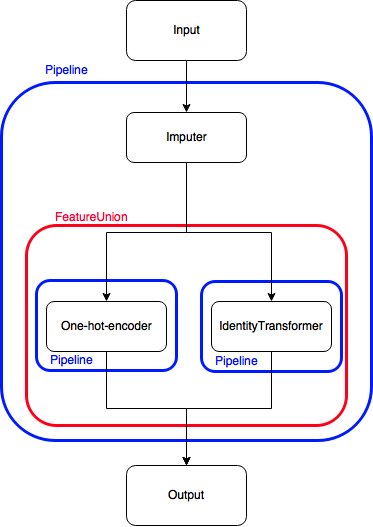
That allows me to have concatenation of the output, without carrying out the same transformation twice! Here’s how I wrote the class, dead-simple:

from sklearn.base import BaseEstimator, TransformerMixin

class IdentityTransformer(BaseEstimator, TransformerMixin):
    def __init__(self):
        pass
    
    def fit(self, input_array, y=None):
        return self
    
    def transform(self, input_array, y=None):
        return input_array*1

That’s it! The ‘magic’ happens in the transform() method: simply multiply by 1. This seems to work for strings as well as for (alpha)numerics. Omitting this *1 seems to throw errors. It’s obvious that the code in itself is not wildly exciting, but it allows me to do some interesting manipulations.

Final thoughts:

• I’m not sure this is the best way to do this. Aside from seeming like an edge case to me, I haven’t extensively tested it on other datasets. It seems to be working fine for this mixed one though. I also don’t know what the performance implications are/could be.
• Before self-rolling transformations left and right, be sure to check sklearn’s documentation on transformers. There’s quite a few that are already part of the package, and they might often already do what you want, several times more efficiently/robustly. I’d be happy to hear any comments if you actually made it to the end of this post.