MixMatch is a form of data augmentation and pseudo-labeling proposed by Google’s Berthelot et al. in their paper MixMatch: A Holistic Approach to Semi-Supervised Learning (arXiv:1905.02249). All it does is essentially combine some already-known techniques for pseudo-labeling, but the paper shows that the act of combining these various techniques leads to significant performance improvements on datasets like CIFAR-10 and CIFAR-100.
The basic premise of pseudo-labeling is that there is knowledge in unlabeled data that we’re currently not leveraging by only using the training set. MixMatch blends labeled and unlabeled data in a way that essentially leads to a more regularised model. Too vague? Let’s hop in. I’ll try to provide a more intuitive explanation at the end of this post.
Note: If you’re not familiar with MixUp, an augmentation technique that MixMatch is based on, it’s best you quickly familiarise yourself with it, perhaps by reading the paper?
Batch Generation Magic
It’s important to understand that pseudo-labeling (and by extension MixMatch) doesn’t touch the architecture of the network that’s being used. It only touches two parts of the processing pipeline: batch generation and of course the loss function. Most of the magic happens during batch generation though, the loss function is just plain old Mean Squared Error (MSE).
So what happens during batch generation?
Essentially, you feed MixMatch two batches, X and U, and it modifies those batches by blending them. X is just your standard batch of training data. U is a batch of your unlabeled data. Let’s forget about X for a second, and focus on what MixMatch does with U.
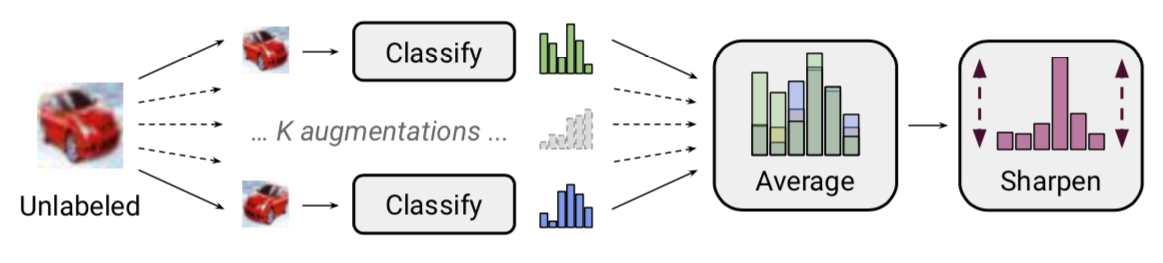
For each element in U, we’ll call it u, MixMatch does the following:
- It augments
utwice, creatingu1andu2(discardingu). The augments are your standard augments like flips and crops for images. - It puts both
u1andu2through the model, and averages the resulting predictions (just a standard average). Let’s call this average distributionq. - Because it wants to lower entropy, it’s going to sharpen up the distribution:
q = Sharpen(q) - The result is that we now have two pseudo-labeled inputs: (
u1, with labelq) and (u2, also with labelq). We’ll throw all of these pseudo-labeled input pairs into one big tensor,pseudoU.
Let’s now blend pseudoU with our X (which has also been augmented with your usual augments, crop, flip etc):
- We’ll throw
XandpseudoUinto one big tensor, and shuffle its order. We’ll call itSuperBatch. - Now we’ll apply MixUp:
- We loop through each input in
X[i], and mix it withSuperBatch[i]. We discard the individual elements fromSuperBatchafter we’ve blended them. - We will also loop through
pseudoU, and mix it with what’s left inSuperBatch. - The paper claims that one of the things that leads to better performance is actually the blending of training data with pseudo labels!
- We loop through each input in
That’s it for MixMatch. We should now have two batches, X_mixedup and U_mixedup. We’ll now feed both of these through the network.
Loss function
This is relatively straightforward:
- For
X_mixedup, it’s just your usual CrossEntropyLoss - For
U_mixedup, we apply MSE. The reason for using MSE is that MSE is bounded, and that it doesn’t care about getting the class right (which is important, as it’s only a pseudo-label!). - The final loss is just a weighted combination:
loss(X_mixedup) + lambda * loss(U_mixedup)
Sane default hyper-parameters
There’s quite a few hyper-parameters for MixMatch, thankfully the researchers propose a couple of good starting points:
- The researchers propose you augment each unlabeled input (
u) only twice (K= 2) - Their proposed augments are just standard crops and flips
- The
Sharpen()function is actually just a “temperature adjustment” where they propose to keep the temperature parameterTat 0.5. - For
lambdain the combined loss function, they propose to start out with a value of 100, but it may have to be adjusted depending on the dataset - For
alpha, which is a parameter that’s relevant to the MixUp operation, they propose to start with 0.75 and adjust depending on the dataset
Intuition: why does MixMatch work?
My understanding of pseudo-labeling in general is shaky to say the least, but I’ll make an attempt at verbalising my understanding so far. In essence, the properties of any good model aren’t limited to “can it reliably classify an input correctly?”. If we take a step back, we can think of a few more properties we want our model to have:
- Predictions of the model should be stable across augmented versions of the same input
- It should be confident in its predictions: one class should have a high predicted probability, while the rest should be negligible in comparison
- The model shouldn’t just memorise its training data, but actually understand what it is being taught
Pseudo-labeling (and thus MixMatch) may not be able to help the model learn to correctly classify, but it can help to teach the model to have the above label-independent meta-properties!
- The data augmentation we apply to
Umakes sure that the model spits out robust predictions across augmentations (note that it doesn’t matter what the model predicts, just that it predicts the same for all augmentations). This is called consistency regularisation. - We teach the model to be confident by sharpening the pseudo-distribution
q. This is what the paper calls entropy minimization. - The random blending performed by MixUp means that the inputs change a bit every time, making it impossible for it to simply memorise the training data. This is just traditional regularisation.
At this stage, you might be worried that the guessed pseudo-labels fromUcould be confusing the legitimate inputs fromXthrough blending. However, MixUp works in such a way that it only adds a “little” of the second mix-in label, it’s still mostly the originalX(say 75-80%).